Phương pháp tìm điều kiện xác định của phương trình và bất

Các em học sinh thân mến, kể từ lớp 8 trở lên, các em sẽ bắt đầu được làm quen với khái niệm phương trình, hệ phương trình, bất phương trình và đây là những kiến thức trọng tâm dành cho các em ôn thi những kỳ thi lớn như kỳ thi lên Trung học phổ thông hay kỳ thi lên Đại học. Để làm được những bài về phương trình hay bất phương trình, điều cơ bản các em cần nắm rõ là tập xác định hoặc điều kiện xác định của phương trình hay bất phương trình ấy là gì. Các em không cần lo lắng, HOCMAI đã chuẩn bị tất cả những kiến thức mà các em cần trong bài viết phương pháp tìm điều kiện xác định.

Bạn Đang Xem: Phương pháp tìm điều kiện xác định của phương trình và bất

A. NHỮNG LÝ THUYẾT CẦN NHỚ

1. Khái niệm phương trình một ẩn

Cho hai hàm số như sau: y = f(x) và y = g(x) có tập xác định lần lượt sẽ là D1 và D2.

Đặt D = D1 ∩ D2. Mệnh đề chứa biến “f(x) = g(x)” được gọi là phương trình một ẩn, x gọi là ẩn và D gọi là tập xác định của phương trình.

Số x0 ∈ D gọi là một nghiệm của phương trình f(x) = g(x) nếu “f(x0) = g(x0)” là một mệnh đề đúng.

2. Phương trình tương đương

Hai phương trình được cho là hai phương trình tương đương khi và chỉ khi chúng có cùng chung một tập nghiệm. Nếu phương trình f1(x) = g1(x) tương đương với phương trình f2(x) = g2(x) thì ta sẽ viết như sau:

f1(x) = g1(x) ⇔ f2(x) = g2(x)

Định lý: Cho hai phương trình f(x) và g(x), cho f(x) = g(x) có tập xác định kí hiệu D và y = h(x) là một hàm số xác định trên tập D. Khi đó trên miền xác định D, phương trình đã cho sẽ tương đương với mỗi phương trình sau đây:

(1) f(x) + h(x) = g(x) + h(x)

(2) f(x).h(x) = g(x).h(x) với h(x) ≠ 0, ∀x ∈ D.

3. Phương trình hệ quả

Phương trình f1(x) = g1(x) có tập nghiệm kí hiệu là S1 được gọi là phương trình hệ quả của phương trình f2(x) = g2(x) có tập nghiệm kí hiệu là S2 nếu S1 ⊂ S2.

Khi đó viết: f1(x) = g1(x) ⇔ f2(x) = g2(x)

Định lý:

Khi bình phương cả 2 vế của một phương trình, ta được phương trình hệ quả của phương trình đã cho như sau: f(x) = g(x) ⇒ 2 = 2

Lưu ý:

– Nếu hai vế của một phương trình luôn luôn cùng dấu thì khi ta bình phương hai vế của nó, ta sẽ có được một phương trình tương đương.

– Nếu như phép chuyển đổi tương đương dẫn đến phương trình hệ quả, ta sẽ phải thử lại các nghiệm tìm được &o phương trình đã cho để phát hiện ra và loại bỏ đi những nghiệm ngoại lai.

4. Phương trình chứa ẩn ở mẫu

Phương trình chứa ẩn ở mẫu là phương trình có biểu thức chứa ẩn ở vị trí mẫu số.

Ví dụ:

2/(x + 3) = 0 là phương trình chứa ẩn ở mẫu (ẩn x)

2 – [4/(y² + 2y + 7)] = 0 là phương trình chứa ẩn ở mẫu (ẩn y)

Ta thấy, việc tìm điều kiện xác định là rất quan trọng trong việc tìm nghiệm của một phương trình. Sau đây, chúng tôi sẽ hướng dẫn phương pháp tìm điều kiện xác định của một phương trình.

5. Phương pháp tìm điều kiện xác định của phương trình

– Điều kiện xác định của phương trình là điều kiện các giá trị của ẩn trong phương trình f(0) được xác định.

Điều kiện xác định của phương trình viết tắt là ĐKXĐ.

– Điều kiện để biểu thức xác định là:

• √f(0) xác định khi f(0) ≥ 0
• 1/f(0) xác định khi f(0) ≠ 0
• 1/√f(0) xác định khi f(0) > 0

B. BÀI TẬP TÌM ĐIỀU KIỆN XÁC ĐỊNH

I. TRẮC NGHIỆM

Câu 1: Tất cả các giá trị của ẩn x để biểu thức √(x – 3) có nghĩa là:

A) x < 3

B) x ≤ 3

C) x > 3

D) x ≥ 3

Đáp án chính xác là: D

Câu 2: Điều kiện xác định của biểu thức √(x – 8) là:

A) x ≥ 8

B) x > 8

C) x < 8

D) x ≤ 8

Đáp án chính xác là: A

Xem Thêm : Kết tủa là gì? Định nghĩa về kết tủa trong hóa học – Bilico Miền Nam

Câu 3: Biểu thức √(2x – 8) có nghĩa khi và chỉ khi:

A) x ≤ -4

B) x ≤ 4

C) x ≥ -4

D) x ≥ 4

Đáp án chính xác là: D

Câu 4: Với x > 0, thì biểu thức nào trong những biểu thức sau đây luôn có nghĩa?

A) √(2 – x)

B) √(x – 2)

C) √(2x)

D) √(-2x)

Đáp án chính xác là: C

Câu 5: Tất cả các giá trị của x để biểu thức √(-x² + 6x – 9) xác định là:

A) x = 6

B) x > 3

C) x = 3

D) x = -3

Đáp án chính xác là: C

Câu 6: Điều kiện xác định của biểu thức √[2017/(x – 2018)] là:

A) x ≥ 2018

B) x ≠ 2018

C) x > 2018

D) x < 2018

Đáp án chính xác là: C

Câu 7: Biểu thức √(1 – y²) xác định khi và chỉ khi:

A) y ≤ 1

B) y ≥ 1

C) -1 ≤ y ≤ 1

D) y ≠ 1

Đáp án chính xác là: C

Câu 8: Điều kiện của x để biểu thức √(3 – x) có nghĩa là:

A) x < 3

B) x ≤ 3

C) x > 3

D) x ≥ 3

Đáp án chính xác là: B

Câu 9: Điều kiện của x để biểu thức √(3x – 6) có nghĩa là:

A) x ≥ -1/2

Xem Thêm : Nhấp ủ có dẫn điện không? Những gì bạn phải biết

B) x ≥ 2

C) x ≥ -2

D) x ≥ 1/2

Đáp án chính xác là: B

Câu 10: Tìm tất cả các giá trị của x để biểu thức P = √(x – 2) được xác định:

A) x < 2

B) x > 2

C) x ≥ 2

D) x ≤ 2

Đáp án chính xác là: C

Câu 11: Để biểu thức P(x) = √(2019 – 3x) + x – 2020 có nghĩa khi:

A) x ≥ 673

B) x ≠ 2020

C) x ≤ 673

D) x < 2019

Đáp án chính xác là: C

Câu 12: Điều kiện để biểu thức M = 1/(√x – 1) xác định là:

A) x > 1

B) x > 0

C) x > 0; x ≠ 1

D) x ≥; x ≠ 1

Đáp án chính xác là: D

II. TỰ LUẬN

Bài 1: Tìm các giá trị x thỏa mãn các điều kiện của mỗi bất phương trình sau đây:

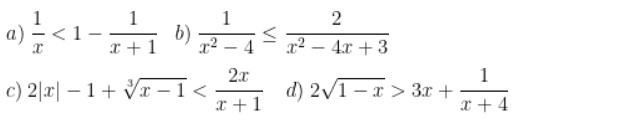
Hướng áp điệu bài:

Bài 2: Chứng minh những bất phương trình sau đây là vô nghiệm:

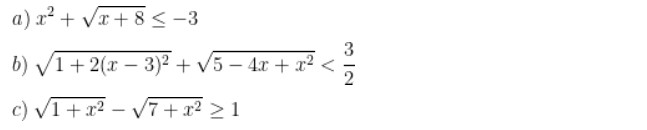
Hướng áp giải bài:

Bài 3: Em hãy giải thích vì sao các cặp bất phương trình sau đây là tương đương?

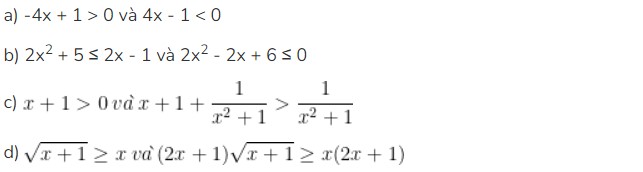
Hướng áp điệu bài:

Bài viết đọc thêm:

Cách giải bất phương trình – Đầy đủ lý thuyết và bài tập

Vậy là bài viết về phương pháp tìm điều kiện xác định đã kết thúc, cũng không quá khó đúng không các em học sinh thân mến. HOCMAI rất mong muốn các em nắm rõ được lý thuyết và áp dụng 1 cách dễ dàng &o các bài tập trên lớp và đề kiểm tra, đề thi của mình. Các em đừng quên truy cập &o hoctot.hocmai.vn nhé, mọi kiến thức các em cần tìm sẽ đều có ở đây.