Góc giữa hai đường thẳng trong không gian – O₂ Education

1. Góc giữa hai đường thẳng trong không gian là gì?

Trong không gian cho 2 đường thẳng a, b bất kỳ. Từ một điểm O nào đó ta vẽ 2 đường thẳng a’, b’ lần lượt song song với a và b. Ta nhận thấy rằng khi điểm O thay đổi thì góc giữa 2 đường thẳng a và b không chuyển biến.

Bạn Đang Xem: Góc giữa hai đường thẳng trong không gian – O₂ Education

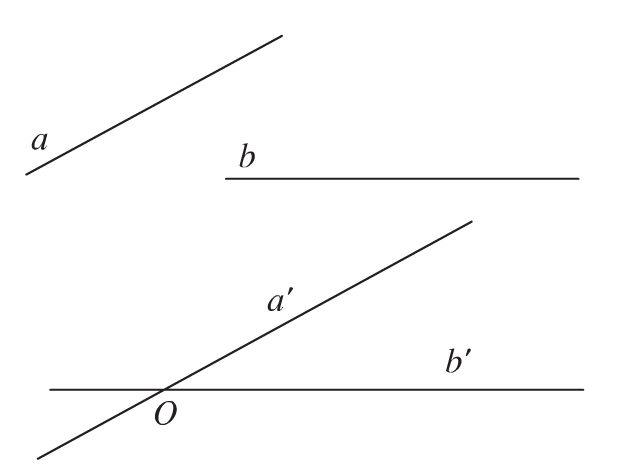
Định nghĩa: Góc giữa hai đường thẳng trong không gian là góc giữa 2 đường thẳng cùng đi qua một điểm và lần lượt song song với hai đường thẳng đã cho.

tìm hiểu thêm:

• phương pháp tính góc giữa đường thẳng và mặt bằng lớp 11
• Cách tính góc giữa hai mặt bằng trong không gian

2. Cách xác định góc giữa hai đường thẳng

Ngoài việc làm như trong định nghĩa, để xác định góc giữa 2 đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.

Hoặc ta có thể sử dụng tích vô hướng:

• Nếu (overrightarrow{u}) là vecto chỉ phương của đường thẳng a và (overrightarrow{v}) là vecto chỉ phương của đường thẳng b và (left( overrightarrow{u};overrightarrow{v} right)=alpha ) thì góc giữa 2 đường thẳng a và b bằng (alpha ) nếu (0le alpha le 90^circ ) và bằng (180{}^circ -alpha ) nếu (90^circ <alpha le 180^circ ).
• Nếu 2 đường thẳng a và b song song hoặc trùng nhau thì góc giữa chúng bằng (0^circ ). Góc giữa 2 đường thẳng là góc có số đo (0le alpha le 90^circ ).

3. Cách tính góc giữa hai đường thẳng

Để tính được góc giữa hai đường thẳng trong không gian, nếu xác định (dựng) được góc giữa hai đường thẳng trong không gian và gắn chúng &o một tam giác cụ thể thì có thể sử dụng các hệ thức lượng trong tam giác để tìm số đo của góc đó:

• Định lý hàm số cosin trong tam giác ABC: (cos widehat{BAC}=frac{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}{2.AB.AC})
• Tương tự ta có: (cos widehat{ABC}=frac{B{{A}^{2}}+B{{C}^{2}}-A{{C}^{2}}}{2.BA.BC}) và (cos widehat{ACB ACB}=frac{C{{A}^{2}}+C{{B}^{2}}-A{{B}^{2}}}{2.CA.CB}) Chú ý: (overrightarrow{AB}.overrightarrow{AC}=AB.ACcos widehat{BAC}=frac{1}{2}left( A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}} right))

Dường như, để tính góc giữa hai véc-tơ $vec{u}, vec{v} $ chúng ta sử dụng định nghĩa tích vô hướng: $$vec{u} . vec{v} = |vec{u}|.|vec{v}|.cos(left( overrightarrow{u};overrightarrow{v} right)$.

Tính góc giữa hai đường thẳng AB và CD ta tính góc giữa hai vectơ (overrightarrow{AB}) và (overrightarrow{CD}) dựa &o công thức (cos left( overrightarrow{AB};overrightarrow{CD} right)=frac{overrightarrow{AB}.overrightarrow{CD}}{left| overrightarrow{AB} right|.left| overrightarrow{CD} right|}Rightarrow cos left( AB;CD right)=frac{left| overrightarrow{AB}.overrightarrow{CD} right|}{left| overrightarrow{AB} right|.left| overrightarrow{CD} right|}) từ đó suy ra góc giữa hai đường thẳng AB và CD.

4. Bài tập góc giữa hai đường thẳng trong không gian

Ví dụ 1. Cho hình lập phương $A B C D cdot A^{prime} B^{prime} C^{prime} D^{prime}$ có cạnh là $a$. Tính góc giữa các cặp đường thẳng sau đây:

1. $A B$ và $A^{prime} D^{prime}$.
2. $A D$ và $A^{prime} C^{prime}$.
3. $B C^{prime}$ và $B^{prime} D^{prime}$.

Lời giải.

1. Ta có $A^{prime} D^{prime} / / A D$ nên $left(A B, A^{prime} D^{prime}right)=(A B, A D)=widehat{B A D}=90^{circ}$.
2. Ta có $A^{prime} C^{prime} / / A C$ nên $left(A D, A^{prime} C^{prime}right)=(A D, A C)=widehat{D A C}=45^{circ}$.
3. Ta có $B^{prime} D^{prime} / / B D$ nên $left(B C^{prime}, B^{prime} D^{prime}right)=left(B C^{prime}, B Dright)=widehat{D B C^{prime}}$. Ta có $B D=B C^{prime}=C^{prime} D=A B sqrt{2}$ nên $triangle B D C^{prime}$ dều, suy ra $widehat{D B C^{prime}}=60^{circ}$. Vậy $left(B C^{prime}, B^{prime} D^{prime}right)=60^{circ}$.

Ví dụ 2. Cho hình chóp $S . A B C$ có $S A=S B=S C=A B=A C=a sqrt{2}$ và $B C=2 a$. Tính góc giữa hai đường thẳng $A C$ và $S B$.

Lời giải.

Xem Thêm : Ông lão đánh cá và con cá &ng – Truyện cổ tích

Ta có $S A B$ và $S A C$ là tam giác đều, $A B C$ và $S B C$ là tam giác vuông cân cạnh huyền $B C$. Gọi $M, N, P$ lần lượt là trung điểm của $S A, A B, B C$, ta có $M N / / S B, N P / / A C$ nên $(A C, S B)=(N P, M N)$.

begin{aligned} &M N=frac{S B}{2}=frac{a sqrt{2}}{2}, N P=frac{A C}{2}=frac{a sqrt{2}}{2} . &A P=S P=frac{B C}{2}=a, S A=a sqrt{2} end{aligned}

Ví dụ 3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, (SAbot left( ABC right)) và (SA=asqrt{3}). Gọi M, N lần lượt là trung điểm của AB và SC. Tính cosin góc giữa hai đường thẳng AN và CM.

Cách 1: Dựng hình bình hành AMCE suy ra (AM=CE=frac{a}{2}).

Khi đó (AE//CMRightarrow left( widehat{AE;CM} right)=left( widehat{AN;AE} right)=varphi .)

Mặt khác (SC=sqrt{S{{A}^{2}}+A{{C}^{2}}}=2aRightarrow ) độ dài đường trung tuyến AN là (AN=frac{SC}{2}=a.AE=CM=frac{asqrt{3}}{2}.)

Do (Delta ABC) đều nên (CMbot AMRightarrow ) AMCE là hình chữ nhật.

Khi đó (CEbot AE) mà (CEbot SARightarrow CEbot left( SAE right)Rightarrow CEbot SE.)

(Delta SEC) vuông tại E có đường trung tuyến (EN=frac{1}{2}SC=a.)

Ta có: (cos widehat{NAE}=frac{A{{N}^{2}}+A{{E}^{2}}-N{{E}^{2}}}{2.AN.AE}=frac{sqrt{3}}{4}>0Rightarrow cos varphi =frac{sqrt{3}}{4}.)

Cách 2: Ta có: (overrightarrow{AN}=frac{1}{2}left( overrightarrow{AS}+overrightarrow{AC} right);overrightarrow{CM}=overrightarrow{AM}-overrightarrow{AC}=frac{1}{2}overrightarrow{AB}-overrightarrow{AC}.)

Khi đó (overrightarrow{AN}.overrightarrow{CM}=frac{1}{2}left( overrightarrow{AS}+overrightarrow{AC} right)left( frac{1}{2}overrightarrow{AB}-overrightarrow{AC} right)=frac{1}{4}overrightarrow{AB}.overrightarrow{AC}-frac{1}{2}A{{C}^{2}}=frac{1}{4}{{a}^{2}}cos 60{}^circ -frac{{{a}^{2}}}{2}=frac{-3{{a}^{2}}}{8}.)

Lại có: (AN=frac{SC}{2}=a;CM=frac{asqrt{3}}{2}Rightarrow cos varphi =frac{left| frac{-3{{a}^{2}}}{8} right|}{a.frac{asqrt{3}}{2}}=frac{sqrt{3}}{4}.)

Xem Thêm : Vì sao có nếp nhăn dưới mắt? 6 Cách cải tổ nhanh rõ rệt

phản hồi: Dựa &o hai cách làm trên ta thấy rằng, trong một số trường hợp, việc sử dụng công cụ vectơ để tính góc giữa hai đường thẳng giúp bài toán trở nên dễ ràng hơn rất nhiều!.

Ví dụ 4. Cho hình chóp S.ABC có (SA=SB=SC=AB=a;AC=asqrt{2}) và (BC=asqrt{3}). Tính cosin góc giữa hai đường thẳng SC và AB.

Cách 1: Gọi M, N, P lần lượt là trung điểm của SA, SB và AC. Khi đó (left{ begin{align}

& MP//SC

& N//AB

end{align} right.Rightarrow left( widehat{SC;AB} right)=left( widehat{MP;MN} right).)

Ta có: (MN=frac{AB}{2}=frac{a}{2};MP=frac{SC}{2}=frac{a}{2}.)

Mặt khác (Delta SAC) vuông tại S (Rightarrow SP=frac{AC}{2}=frac{asqrt{2}}{2}.)

(B{{P}^{2}}=frac{B{{A}^{2}}+B{{C}^{2}}}{2}-frac{A{{C}^{2}}}{4}=frac{3}{2}{{a}^{2}}Rightarrow BP=frac{asqrt{6}}{2}.)

Suy ra (P{{N}^{2}}=frac{P{{S}^{2}}+P{{B}^{2}}}{2}-frac{S{{B}^{2}}}{4}=frac{3{{a}^{2}}}{4}Rightarrow NP=frac{asqrt{3}}{2}.)

Khi đó (cos widehat{NMP}=frac{M{{N}^{2}}+M{{P}^{2}}-N{{P}^{2}}}{2.MN.MP}=-frac{1}{2}Rightarrow widehat{NMP}=120{}^circ Rightarrow varphi =left( widehat{SC;AB} right)=60{}^circ .)

Cách 2: Ta có: (overrightarrow{AB}=overrightarrow{SB}-overrightarrow{SA}Rightarrow overrightarrow{AB}.overrightarrow{SC}=left( overrightarrow{SB}-overrightarrow{SA} right).overrightarrow{SC}=overrightarrow{SB}.overrightarrow{SC}-overrightarrow{SA}.overrightarrow{SC})

(=frac{1}{2}left( S{{B}^{2}}+S{{C}^{2}}-A{{C}^{2}} right)-frac{1}{2}left( S{{A}^{2}}+S{{C}^{2}}-A{{B}^{2}} right)=-frac{{{a}^{2}}}{2}.)

Suy ra (cos left( SC;AB right)=frac{left| frac{-{{a}^{2}}}{2} right|}{a.a}=frac{1}{2}Rightarrow left( SC;AB right)=60{}^circ .)