Bất đẳng thức Côsi và ứng dụng – O₂ Education

Bất đẳng thức CôSi (Cauchy) hay bất đẳng thức AM-GM là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm.

Bạn Đang Xem: Bất đẳng thức Côsi và ứng dụng – O₂ Education

1. Bất đẳng thức Cô-si là gì?

Trong toán học, bất đẳng thức Cauchy là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm được phát biểu như sau.

Với $a_1,a_2,ldots,a_n$ là các số thực không âm, khi đó $$a_1+a_2+cdots +a_{n}ge nsqrt[n]{a_1a_2ldots a_n}.$$ Dấu bằng xảy ra khi và chỉ khi $a_1=a_2=cdots =a_n$.

Các trường hợp đặc biệt của bất đẳng thức Cosi:

• Bất đẳng thức Cô si với 2 số thực không âm $a$ và $b$ thì: [frac{a+b}{2} geqslant sqrt{ab}] Dấu “=” xảy ra khi và chỉ khi a = b.
• Bất đẳng thức Cô si với 3 số thực không âm $a,b$ và $c$ thì: [frac{a+b+c}{3} geqslant sqrt[3]{abc}] Dấu “=” xảy ra khi và chỉ khi a = b =c.

Tên đúng của bất đẳng thức này là bất đẳng thức AM-GM. Có nhiều cách để chứng minh bđt này nhưng hay nhất là cách chứng minh quy nạp của Cauchy.

2. Các dạng phát biểu của bất đẳng thức Cô-si

a. Dạng bao quát của bất đẳng thức Cô-si

Cho $x_1, x_2, x_3,…,x_n$ là các số thực dương ta có:

– Dạng 1: (dfrac{x_1+x_2+…+x_n}{n} geqslant sqrt[n]{x_1 x_2 x_3…x_n})

– Dạng 2: ({x_1+x_2+…+x_n} geqslant nsqrt[n]{x_1 x_2 x_3…x_n})

– Dạng 3: (left(dfrac{x_1+x_2+…+x_n}{n}right)^n geqslant x_1 x_2 x_3…x_n)

– Dạng 4: (left(x_1+x_2+…+x_nright)left(frac{1}{x_1}+frac{1}{x_2}+…frac{1}{x_n} right) geqslant n^2)

Dấu đẳng thức xảy ra khi và chỉ khi $x_1= x_2= x_3=…=x_n$.

b. Dạng đặc biệt của bất đẳng thức Cô-si

Là các trường hợp đặc biệt của dạng tổng quát ở trên khi n=2, n=3.

c. Một số bất đẳng thức được suy ra từ bất đẳng thức Cauchy

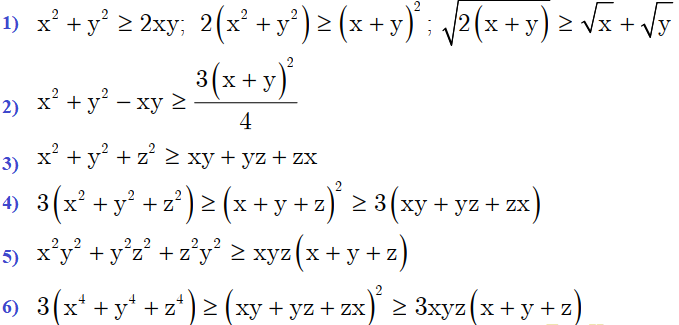
d. Chú ý khi sử dụng bất đẳng thức AM – GM

• Khi áp dụng bất đẳng thức Cô si thì các số phải là những số không âm;
• Bất đẳng thức Côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích;
• Điều kiện xảy ra dấu ‘=’ là các số bằng nhau;
• Bất đẳng thức Côsi còn có hiệ tượng khác thường hay sử dụng.

3. Hệ quả của bất đẳng thức Cô-si

• (x^{2}+y^{2} geq 2 x y ; 2left(x^{2}+y^{2}right) geq(x+y)^{2} ; sqrt{2(x+y)} geq sqrt{x}+sqrt{y})
• (x^{2}+y^{2}-x y geq frac{3(x+y)^{2}}{4})
• (x^{2}+y^{2}+z^{2} geq x y+y z+z x)
• (3left(x^{2}+y^{2}+z^{2}right) geq(x+y+z)^{2} geq 3(x y+y z+z x))
• (x^{2} y^{2}+y^{2} z^{2}+z^{2} y^{2} geq x y z(x+y+z)+3left(x^{4}+y^{4}+z^{4}right) geq(x y+y z+z x)^{2} geq 3 x y z(x+y+z))

4. Các dạng bài tập bất đẳng thức Cô-si

Bài 1: Tìm giá trị bé nhất của biểu thức $A=x+frac{7}{x}$ với x > 0.

Lời giải:

Áp dụng bất đẳng thức Cô si cho hai số x > 0 và ta có: [ x+frac{7}{x} geq 2 sqrt{x cdot frac{7}{x}}=2 sqrt{7} ] Dấu “=” xảy ra khi và chỉ khi (x=frac{7}{x} Leftrightarrow x^{2}=7 Leftrightarrow x=sqrt{7}) (do x>0).

Xem Thêm : Chủ nghĩa Mác-Lênin, tư tưởng Hồ Chí Minh mãi mãi soi sáng con

Vậy (min A=2 sqrt{7} Leftrightarrow x=sqrt{7}).

Bài 2: Cho (x>0, y>0) thỏa mãn điều kiện (frac{1}{x}+frac{1}{y}=frac{1}{2}). Tìm giá trị lớn nhất của biểu thức (A=sqrt{x}+sqrt{y}).

Lời giải: Áp dụng bdt Cosi ta có [ frac{1}{x}+frac{1}{y} geq 2 sqrt{frac{1}{x} cdot frac{1}{y}} Leftrightarrow frac{1}{2} geq frac{2}{sqrt{x y}} Leftrightarrow sqrt{x y} geq 4 ]Lại có, áp dụng bất đẳng thức Cô si cho hai số (x>0, y>0) ta có:[sqrt{x}+sqrt{y} geq 2 sqrt{sqrt{x y}}=2 sqrt{4}=4 ] Dấu “=” xảy ra khi và chỉ khi [ left{begin{array}{l}x=y frac{1}{x}+frac{1}{y}=frac{1}{2}end{array} right. Leftrightarrow x=y=4. ]

Vậy $min A = 4$ khi và chỉ khi $x = y = 4$.

Bài 3: Ví dụ: Cho (a), (b) là số dương thỏa mãn (a^{2}+b^{2}=2). Chứng minh rằng [ (a+b)^{5} geq 16 a b sqrt{left(1+a^{2}right)left(1+b^{2}right)} ]

Lời giải: Ta có ((a+b)^{5}=left(a^{2}+2 a b+b^{2}right)left(a^{3}+3 a b^{2}+3 a^{2} b+b^{3}right))

Áp dụng bdt Côsi ta có [ begin{aligned} &a^{2}+2 a b+b^{2} geq 2 sqrt{2 a bleft(a^{2}+b^{2}right)}=4 sqrt{a b} text { và } &left(a^{3}+3 a b^{2}right)+left(3 a^{2} b+b^{3}right) geq 2 sqrt{left(a^{3}+3 a b^{2}right)left(3 a^{2} b+b^{3}right)}=4 sqrt{a bleft(1+b^{2}right)left(a^{2}+1right)} end{aligned} ]

Suy ra (left(a^{2}+2 a b+b^{2}right)left(a^{3}+3 a b^{2}+3 a^{2} b+b^{3}right) geq 16 a b sqrt{left(a^{2}+1right)left(b^{2}+1right)})

Do đó ((a+b)^{5} geq 16 a b sqrt{left(1+a^{2}right)left(1+b^{2}right)}) (đpcm). Đẳng thức xảy ra khi và chỉ khi (a=b=1).

Bài 4: Tìm GTLN của: $y=x^{2}(1-x) quad, x in(0,1)$

Lời giải: Do $x, 1-x>0$ nên áp dụng bất đẳng thức Cauchy ta có: $$ 2 y=x^{2}(1-2 x)=x cdot x cdot(1-2 x) leqleft(frac{x+x+1-2 x}{3}right)^{3}=frac{1}{27} Rightarrow y leq frac{1}{54} $$ Dấu ‘=’ xảy ra $Leftrightarrow x=1-2 x Leftrightarrow x=frac{1}{3}$.

Vậy Max $y=frac{1}{27}$ khi $x=frac{1}{3}$

Bài 5: Tìm GTNN của: $y=x+frac{1}{x-1}, x>1$.

Lời giải: Do $x-1>0$ nên áp dụng bất đẳng thức Cauchy ta có: $$ y=(x-1)+frac{1}{x-1}+1 geq 2 sqrt{(x-1) cdot frac{1}{x-1}}+1=3 Rightarrow y geq 3 $$ Dấu ‘=’ xảy ra $Leftrightarrow x-1=frac{1}{x-1} Leftrightarrow x=2$.

Vậy Min $y=3$ khi $x=2$.

bài viết liên quan Chọn điểm rơi trong bất đẳng thức Côsi (Cauchy).

Bài 6: Cho 3 số dương (a, b), c, hãy chứng minh: [ left(a+frac{1}{b}right)left(b+frac{1}{c}right)left(c+frac{1}{a}right) geq 8 ]

Xem Thêm : Tính chất của Oxi (O2): Tính chất hóa học, vật lí, Điều chế, Ứng dụng

Hướng dẫn giải: Áp dụng BĐT Cosi, ta có: [ begin{aligned} a+frac{1}{b} geq 2 sqrt{frac{a}{b}}; b+frac{1}{c} geq 2 sqrt{frac{b}{c}}; c+frac{1}{a} geq 2 sqrt{frac{c}{a}} end{aligned}]

Nhân theo vế 3 bdt này ta được [left(a+frac{1}{b}right)left(b+frac{1}{c}right)left(c+frac{1}{a}right) geq 8 sqrt{frac{a}{b}} cdot sqrt{frac{b}{c}} sqrt{frac{c}{a}}=8 ] Đẳng thức xảy ra khi và chỉ khi (a=b=c).

Bài 7: Cho $a, b, c>0$. Chứng minh:

a) $a^2+b^2+4 geqslant 2a+2b+ab$b) $a(1+b)+b(1+c)+c(1+a) geq 3 sqrt[3]{a b c}(1+sqrt[3]{a b c})$c) $a sqrt{b-1}+b sqrt{a-1} leq a b$ với $a, b geq 1$

Lời giải:

a) Áp dụng bât đẳng thức Cauchy ta có: $$ begin{aligned} &a^{2}+4 geq 4 a &b^{2}+4 geq 4 b &a^{2}+b^{2} geq 2 a b. end{aligned} $$ Cộng lại ta được: $$ 2 a^{2}+2 b^{2}+8 geq 4 a+4 b+2 a b $$ Dấu ‘=’ xảy ra $ Leftrightarrow a=b=2$

b) Ta có : $$ a(1+b)+b(1+c)+c(1+a)=(a+b+c)+(a b+b c+c a) $$ Áp dụng bất đẳng thức Cauchy : $$ begin{aligned} &a+b+c geq 3 sqrt[3]{a b c} &a b+b c+c a geq 3 sqrt[3]{a^{2} b^{2} c^{2}} end{aligned} $$ Cộng lại ta được đpcm.

Dấu ‘=’ xảy ra $Leftrightarrow a=b=c$.

c) Ta có: $$a sqrt{b-1}=sqrt{a} sqrt{a b-a} leq frac{a+a b-a}{2}=frac{a b}{2}$$Tương tự: $$b sqrt{a-1} leq frac{a b}{2}$$ Cộng lại ta đpcm.

Dấu ‘=’ xảy ra $Leftrightarrow a=b=2$.

Bài 8: Chứng minh với ba số a, b, c không âm thỏa mãn a + b + c = 3 thì: [ frac{a}{b+c}+frac{b}{c+a}+frac{c}{a+b} geq frac{3}{2} ]

Nhận xét: Bài toán đạt được dấu bằng khi và chi khi $a = b = c = 1$.

Ta sẽ sử dụng phương pháp làm trội làm giảm như sau: [ frac{a}{b+c}+frac{b+c}{4}+frac{1}{2 a} geq 3 sqrt[3]{frac{a}{b+c} cdot frac{b+c}{4} cdot frac{1}{2 a}}=3 sqrt[3]{frac{1}{8}}=frac{3}{2} ]

Tương tự ta có (frac{b}{c+a}+frac{c+a}{4}+frac{1}{2 b} geq frac{3}{2}) và (frac{c}{a+b}+frac{a+b}{4}+frac{1}{2 c} geq frac{3}{2}).

Cộng vế với vế ta có: [ begin{align*}frac{a}{b+c}+frac{b+c}{4}+frac{1}{2 a}+frac{b}{c+a}+frac{c+a}{4}+frac{1}{2 b}+frac{c}{a+b}+frac{a+b}{4}+frac{1}{2 c} & geq 3 cdot frac{3}{2}=frac{9}{2} Leftrightarrow frac{a}{b+c}+frac{b}{c+a}+frac{c}{a+b}+frac{2(a+b+c)}{4}+frac{a b+b c+c a}{2 a b c} & geq frac{9}{2} Leftrightarrow frac{a}{b+c}+frac{b}{c+a}+frac{c}{a+b}+frac{a+b+c}{2}+frac{a+b+c}{2} & geq frac{9}{2} Leftrightarrow frac{a}{b+c}+frac{b}{c+a}+frac{c}{a+b} &geq frac{9}{2}-3=frac{3}{2} end{align*} ]

Dấu “=” xảy ra khi và chỉ khi $a = b = c = 1$.