Công thức thể tích khối trụ và bài tập có lời giải chính xác 100%

Khối trụ là hình trụ cùng với phần phía bên trong của hình trụ đó. Vậy công thức tính thể tích khối trụ như thế nào? Tất cả sẽ được chúng tôi miêu tả chi tiết trong bài viết dưới đây

Bạn Đang Xem: Công thức thể tích khối trụ và bài tập có lời giải chính xác 100%

xem thêm thêm:

• Công thức tính thể tích khối chóp, các dạng bài tập có lời giải chuẩn 300%

Công thức tính thể tích khối trụ

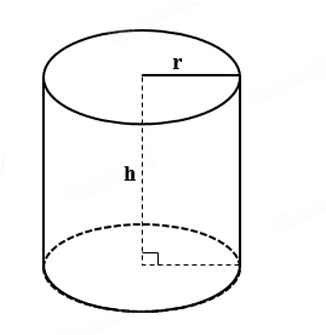
Thể tích khối trụ bằng tích của diện tích mặt đáy và chiều cao. Nói cách khác, thể tích khối trụ bằng chiều cao nhân với bình phương độ dài bán kính hình tròn mặt đáy hình trụ và số pi.

V = S.h = π.r2.h.

Trong đó:

• r là nửa đường kính hình tròn mặt đáy hình trụ
• h là chiều cao của hình trụ
• π là hằng số ( π = 3, 14)
• S là diện tích mặt đáy

Ngoài ra, Anh chị có thể tham khảo công thức tính diện tích bao quanh hình trụ hay toàn phần để ứng dụng giải các bài tập về thể tích hình trụ.

Các dạng bài tập về thể tích khối trụ từ cơ bản đến nâng cao

Trong công thức tính thể tích khối trụ có 3 đại lượng đó là thể tích (V), nửa đường kính đáy (r), và chiều cao (h). Chú ý chiều cao h cũng chính bằng độ dài đường sinh của hình trụ. Từ đó ta có 3 dạng toán sau:

Dạng 1: Tìm chiều cao của hình trụ

Phương pháp:

• Định nghĩa chiều cao hình trụ: Khoảng cách của 2 đáy trên mặt bên.
• Trong trường hợp chưa biết chiều cao của hình trụ, em có thể lấy thước để đo chính xác độ dài của đường cao rồi thay &o công thức là tính được thể tích của hình trụ.

Xem Thêm : Soạn bài Nhà rông ở Tây Nguyên lớp 3 trang 77, 78 sách Cánh Diều

Ví dụ 1: Một hình trụ có chu vi đáy bằng 20 cm, diện tích bao quanh bằng 14 cm2. Tính chiều cao của hình trụ và thể tích của hình trụ.

Lời giải:

Diện tích bao quanh: Sxq = chu vi đáy x chiều cao = 2πrh = 20 x h = 14

=> h = Sxq : chu vi đáy = 14: 20 = 0,7 cm

Mặt khác: Chu vi đáy = 20cm => 2πr = 20 => r = 20 : 2π = ~ 3,18 cm

Thể tích của hình trụ: V = πr2h = 3,14 x (3,18)2 x 0,7 = ~ 219,91 cm3

Dạng 2: Tìm diện tích đáy tròn

Để tìm diện tích đáy tròn, ta áp dụng công thức tính diện tích hình tròn: A = π.r2 với A là kí hiệu diện tích đáy tròn, r là nửa đường kính của hình tròn (mặt đáy hình trụ).

Ví dụ 2: Một hình trụ có diện tích toàn phần gấp 2 lần diện tích bao quanh biết nửa đường kính đáy hình trụ là 6cm. Tính thể tích hình trụ.

Lời giải:

Diện tích toàn phần gấp 2 lần diện tích bao quanh: Stp = 2Sxq

=> 2 x 2 x π x r x h = 2 x π x r x (r + h) => 2h = 6 + h => h = 6 (cm)

Xem Thêm : Vì sao cuộc kháng chiến nhà Hồ Chống quân Minh Thất bại … – Olm

Thể tích của hình trụ: V = π x r2 x h = ~ 678,58 cm3

Dạng 3: Tìm bán kính đáy

Có thể tính bất kì mặt đáy nào vì hai mặt đáy đều bằng nhau. Trong trường hợp chưa biết số đo bán kính đáy, em sử dụng thước để đo khoảng cách mênh mông nhất trên đường tròn rồi lấy kết quả đó chia cho 2 vì r = 1/2.d (d là kí hiệu của đường kính).

Ví dụ 3: Cho khối trụ có thể tích bằng πa³, chiều cao 2a. Tính bán kính đáy của khối trụ.

Ví dụ 4: Cho hình trụ (H) có hai đáy là hai đường tròn tâm O và O’. Điểm A và B lần lượt nằm trên đường tròn (O) và (O’). Biết rằng AB=a và AB tạo với trục OO’ góc α. Khoảng cách giữa AB và OO’ bằng d. Tính theo a và α thể tích khối trụ (H).

Lời giải:

Gọi C là hình chiếu của A lên đường tròn (O’). Gọi I là trung điểm của BC. Dễn thấy ∠BAC là góc giữa dây AB và trục OO’. Tức là ∠BAC=α.

Sau khi đọc xong bài viết của chúng tôi bạn có thể nhớ được công thức tính thể tích khối trụ để vận dụng giải các bài tập nhé