Giải bài 58, 59, 60, 61, 62 trang 99 sgk toán 8 tập 1 – Giaibaitap.me

Bài 58 trang 99 sgk toán 8 tập 1

Bạn Đang Xem: Giải bài 58, 59, 60, 61, 62 trang 99 sgk toán 8 tập 1 – Giaibaitap.me

Điền &o chỗ trống, biết rằng (a, b) là độ dài các cạnh, (d) là độ dài đường chéo của một hình chữ nhật.

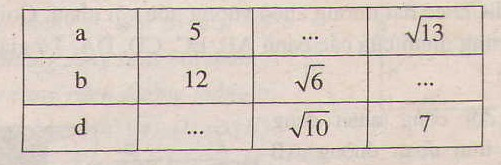
Bài giải:

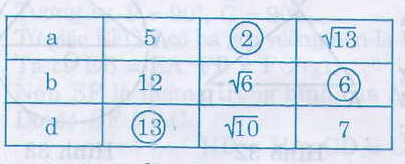
Cột thứ hai:

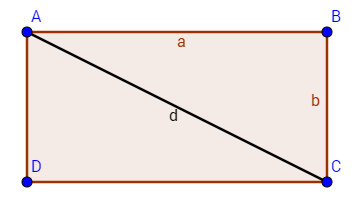
Áp dụng định lí Pytago &o tam giác vuông (ABC) ta có:

({d^{2}} = {rm{ }}{a^2} + {rm{ }}{b^2} = {rm{ }}{5^2} + {rm{ }}{12^2} = {rm{ }}25{rm{ }} + {rm{ }}144{rm{ }} = {rm{ }}169)

Nên (d =sqrt{169}= 13)

Cột thứ ba:

Áp dụng định lí Pytago &o tam giác vuông (ABC) ta có:

({a^2} + {rm{ }}{b^{2}} = {d^2} Rightarrow {a^2} = {rm{ }}{d^2} – {b^2} = (sqrt{10}))2 – ((sqrt{6}))2

(= 10 – 6 = 4Rightarrow a = sqrt 4=2)

Cột thứ tư:

Áp dụng định lí Pytago &o tam giác vuông (ABC) ta có:

({a^2} + {rm{ }}{b^{2}} = {rm{ }}{d^2} Rightarrow {b^2} = {rm{ }}{d^2} – {rm{ }}{a^2} = {rm{ }}{7^2} – (sqrt{13}))2

Xem Thêm : Cách xử lý cơn đau đầu sau khi uống rượu bia – OTiV

(= 49 – 13 = 36)(Rightarrow b=sqrt {36}= 6)

Bài 59 trang 99 sgk toán 8 tập 1

Chứng minh rằng:a) Giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó.

b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.

Bài giải:

a)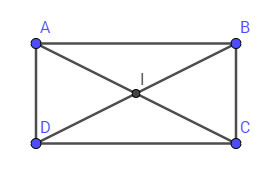

Vì hình bình hành nhận giao điểm hai đường chéo làm tâm đối xứng, mà hình chữ nhật là một hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình.

b)

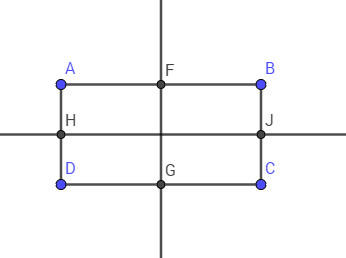
Vì hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng, mà hình chữ nhật là một hình thang cân có hai đáy là hai cạnh đối xứng của hình chữ nhật nên hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó

Bài 60 trang 99 sgk toán 8 tập 1

Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng (7cm) và (24cm).

Bài giải:

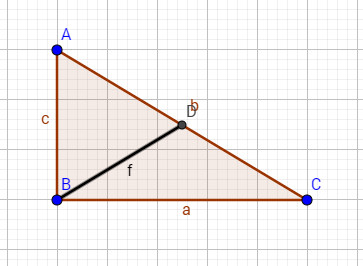
Gọi (b) là độ dài cạnh huyền của tam giác vuông (ABC).

Theo định lí Pitago ta có:

(eqalign{ & {b^2} = {7^2} + {24^2} = 49 + 576 = 625 cr & b = sqrt {625} = 25 cr} )

Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là (12,5cm).

Bài 61 trang 99 sgk Toán 8 tập 1

Xem Thêm : Tập đọc lớp 4 Thưa chuyện với mẹ – Hướng dẫn đọc hiểu – Vuihoc.vn

Cho tam giác (ABC), đường cao (AH). Gọi (I) là trung điểm của (AC, E) là điểm đối xứng với (H) qua (I). Tứ giác (AHCE) là hình gì ? Vì sao ?Bài giải:

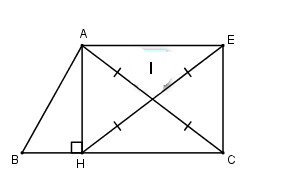
Theo giả thiết (I) là trung điểm của (AC) nên (IA = IC)(E) là điểm đối xứng với (H) qua (I) nên (I) là trung điểm của (HE) hay (IE = IH)

Tứ giác (AHCE) có hai đường chéo cắt nhau tại trung điểm mỗi đường do đó là hình bình hành (theo dấu hiệu nhận biết 5)

Mặt khác (AH) là đường cao nên (widehat{AHC}=90^0)

Do đó (AHCE) là hình chữ nhật (theo dấu hiệu nhận biết 3)

Bài 62 trang 99 sgk toán 8 tập 1

Các câu sau đúng hay sai ?

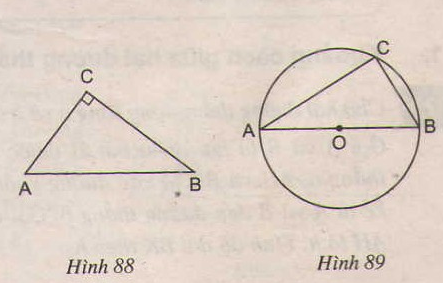
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)

b) Nếu điểm C thuộc đường tròn có đường kính là AB ( C khác A và B) thì tam giác ABC vuông tại C(h.89).

Bài giải

a) Đúng.

Gọi O là trung điểm của AB. Ta có CO là trung tuyến ứng với cạnh huyền nên

(OC = frac{1}{2}AB) hay (OC = OA = OB). Nên A, B, C cùng thuộc đường tròn bán kình OA. Vậy C thuộc đường tròn đường kính AB.

b) Đúng.

Gọi O là tâm đường tròn. Tam giác ABC có trung tuyến CO bằng nửa cạnh AB (do (CO = AO = OB) ) nên tam giác ABC vuông tại C.

Giaibaitap.me